1. divide and conquer와 dynamic programming의 차이
divide and conquer(분할정복)는 하나의 문제를 해결할 수 있을 정도의 작은 부분으로 분할하여 하나하나 정복해나가는 프로그래밍 기법을 말합니다. 작게 나눌수록 복잡해 보였던 문제는 단순화되고 보다 쉽게 해결책을 도출해낼 수 있게 됩니다.
dynamic programming(동적계획법)은 문제를 작은 조각들로 분해하여 한꺼번에 해결한다는 점에서 분할정복과 유사해보입니다. 하지만 분명한 차이가 있습니다. 분할정복은 하나의 문제를 작은 문제들로 나누고, 그 작은 문제들을 해결한 결과를 합쳐나가는 방식으로 문제에 대한 최종 해를 구하는 것인 반면, 다이내믹 프로그래밍은 일련의 문제들을 해결하기 위해서 문제를 작은 조각들로 분할하고, 조각들을 최대한 재활용하여 효율적으로 한번에 해결하는 것입니다.
이게 무슨 소리인가 싶으시겠죠. 예를 보면 조금 더 이해가 쉽습니다.
피보나치 수열은 1 1 2 3 5 8 13 21과 같이 자신보다 앞에 있는 두 숫자를 더한 것과 자기 자신이 같은 수열을 말합니다.
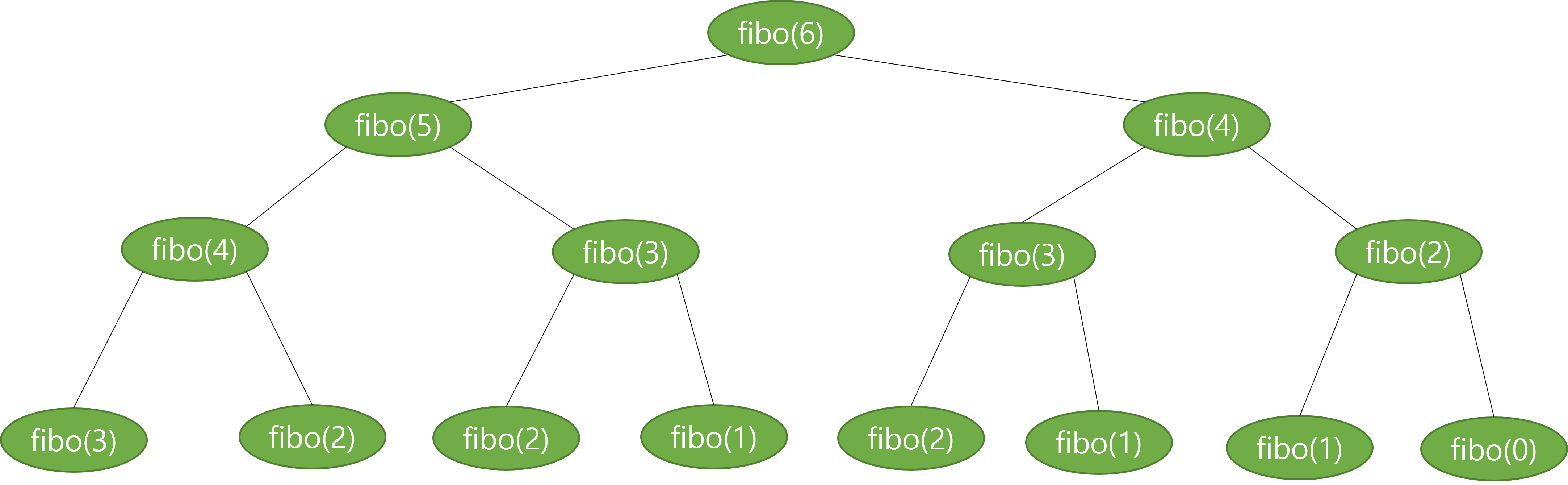
분할 정복을 이용해서 피보나치 수열 인덱스 6번의 값, fibo(6)을 구하는 방법은 다음과 같습니다.
public static int fibo(int n) {
if(n == 0 || n == 1) return 1;
return fibo(n - 2) + fibo(n - 1);
}
fibo(6)이라는 문제를 fibo(5)과 fibo(4)라는 작은 문제로 분할했습니다.
다시 fibo(5)와 fibo(4)를 구하기 위해서 각각 fibo(4)와 fibo(3), fibo(3)과 fibo(2)를 해결해야 합니다.
이런 식으로 매우 쉽게 문제를 해결할 수 있습니다. (컴퓨터는 조금 고생을 하겠지만...)
위에서 알 수 있듯이 분할정복은 재귀적입니다. 분할된 작은 문제들이 중복될 수 있고, 따라서 자원을 낭비하게 됩니다.
반면, 다이내믹 프로그래밍은 중복된 연산을 제거함으로써 효율성을 높일 수 있습니다. optimization, 즉 최적해를 찾는 것이 다이나믹 프로그래밍의 목적이라고 할 수 있습니다.
2. 방법론
구체적으로 다이나믹 프로그래밍을 활용하는 방법에는 다음 두 가지가 있습니다.
Memoization - Top-down - 하향식
메모이제이션은 문제를 해결하는 과정에서 중간 결과를 저장해나가는 방법입니다.
피보나치수열의 예를 다시 살펴봅시다.
계산결과를 저장할 배열 mem []을 준비합니다.
fibo(6)은 함수 fibo(5)와 fibo(4)를 호출하게 되는데, 이때 mem에 mem [5]와 mem[4]가 존재하는 지 확인합니다.
값이 없다면 fibo(5)와 fibo(4)를 계산한 결과를 각각 mem[5]와 mem [4]에 저장해 줍니다.
이런 식으로 fibo(n)을 한 번만 계산하고 다음부터는 mem에 저장된 값을 활용하여 실행시간을 단축시킬 수 있습니다.
구하고자 하는 문제 fibo(6)으로부터 내려오는 방식이기 때문에 Top-down이라고 합니다.
Tabulation - Bottom-up - 상향식
타뷸레이션은 밑에서부터 최종 결과를 구할 때까지 표를 만들어 나가는 방식입니다.
| fibo[0] | fibo[1] | fibo[2] | fibo[3] | fibo[4] | fibo[5] | fibo[6] |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 |
3. 대표적인 문제와 알고리즘들
최장 부분수열 구하기
냅색 알고리즘
벨만-포드 알고리즘 / 플로이드-워셜 알고리즘
...
참조 :
https://www.interviewbit.com/blog/difference-between-divide-and-conquer-and-dynamic-programming/
'Computer Science > Algorithms' 카테고리의 다른 글
| 선택정렬, 버블정렬, 삽입정렬 (0) | 2021.11.09 |
|---|---|
| 스택과 괄호의 값 (0) | 2021.11.04 |
| 그리디 알고리즘? (0) | 2021.11.04 |
| 완전탐색 - 순열 (0) | 2021.11.03 |
| 피보나치 함수 카운팅 (0) | 2021.11.01 |


댓글